二分算法

二分算法思想

其实很多人认为只有具有单调性的数列才能用二分，其实不是。

单调序列一定能二分，能二分的却不一定时单调序列。

二分的实质其实是根据元素集合中的某种性质来找出性质的边界。

基本步骤为：

1、确定分界点，一般为mid = l + r >> 1

2、确定分界点的判断函数check()

3、根据判断结果的真和假来划分区间

二分模板

整型

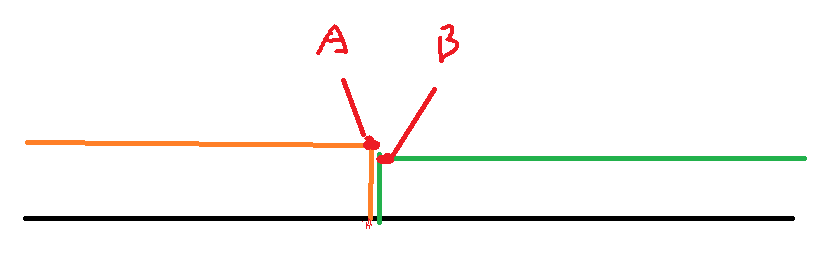
整型二分的模板右两种

1、想找出边界的第一个点(例如 图中的B点)

假设想找出最后一个小于等于 X 的点

while(l < r){
    int mid = l + r >> 1;//1、确定分界点
    if (mid >= x) r = mid;//2、确定判断函数；3、划分区间
    else l = mid + 1;
} 

注：这里只是举了一个具体的例子，实际上如果将区间[l,r]划分区间为[l，mid]或[mid + 1, r] 都可使用

2、想找出边界的最后一个点（例如 如中的A点）

假设想找出第一个大于等于 X 的点

while(l < r){
    int mid = l + r + 1 >> 1; //注意这里加了1
    if(mid <= x) l = mid;
    else r = mid - 1;
}

因为c++中除法是向下取整，如果此时r = l + 1那么此时更新区间左端点的步骤l = mid实际没有作用，会陷入死循环中

注：这里只是举了一个具体的例子，实际上如果将区间[l,r]划分区间为[l，mid - 1]或[mid , r] 都可使用

浮点型

浮点型就要简单多了，没那么多的区间限制

while(l < r){
    int mid = l + r >> 1;
    if (check(mid)) r= mid;
    else l = mid;
}

巨简单！